1708번: 볼록 껍질
첫째 줄에 점의 개수 N(3 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 점의 x좌표와 y좌표가 빈 칸을 사이에 두고 주어진다. 주어지는 모든 점의 좌표는 다르다고 가정해도 좋다. x��
www.acmicpc.net
문제
다각형의 임의의 두 꼭짓점을 연결하는 선분이 항상 다각형 내부에 존재하는 다각형을 볼록 다각형이라고 한다. 아래 그림에서 (a)는 볼록 다각형이며, (b)는 볼록 다각형이 아니다.
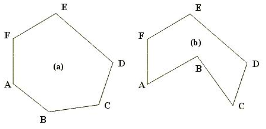
조금만 생각해 보면 다각형의 모든 내각이 180도 이하일 때 볼록 다각형이 된다는 것을 알 수 있다. 편의상 이 문제에서는 180도 미만인 경우만을 볼록 다각형으로 한정하도록 한다.
2차원 평면에 N개의 점이 주어졌을 때, 이들 중 몇 개의 점을 골라 볼록 다각형을 만드는데, 나머지 모든 점을 내부에 포함하도록 할 수 있다. 이를 볼록 껍질 (CONVEX HULL) 이라 한다. 아래 그림은 N=10인 경우의 한 예이다.
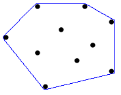
점의 집합이 주어졌을 때, 볼록 껍질을 이루는 점의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 점의 개수 N(3 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 점의 x좌표와 y좌표가 빈 칸을 사이에 두고 주어진다. 주어지는 모든 점의 좌표는 다르다고 가정해도 좋다. x좌표와 y좌표의 범위는 절댓값 40,000을 넘지 않는다. 입력으로 주어지는 다각형의 모든 점이 일직선을 이루는 경우는 없다.
출력
첫째 줄에 볼록 껍질을 이루는 점의 개수를 출력한다.
볼록 껍질의 변에 점이 여러 개 있는 경우에는 가장 양 끝 점만 개수에 포함한다.
예제 입력 1
8
1 1
1 2
1 3
2 1
2 2
2 3
3 1
3 2
예제 출력 1
5
접근
스택을 이용한 "그라함 스캔"과 반시계방향 정렬을 위한 "CCW" 을 이용하는 대표적 Convex Hull 알고리즘 문제이다.
또 이문제는 int로 받아주면 오버플로가 나서 각 좌표를 long으로 받아줘야 한다. 자세한 설명은 주석으로!
코드
import java.io.*;
import java.util.*;
class Main{
static int n;
// x, y 절대값은 절대 40,000을 넘지 않음
static Point first = new Point(40001, 40001);
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
List<Point> points = new ArrayList<Point>();
for(int i=0; i<n; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
points.add(new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
}
// 점들 중, x좌표값이나, y좌표값이 가장 작은 점을 기준점으로 잡는다
for(int i=0; i<points.size(); i++){
if(points.get(i).y < first.y){
first = points.get(i);
} else if(points.get(i).y == first.y){
if(points.get(i).x < first.x)
first = points.get(i);
}
}
// 기준점과 나머지 점들이 ccw로 반시계방향(좌회전)이 되도록 정렬을 시키고, 만약 일직선상에 있으면 거리가 증가하게끔 정렬한다.
points.sort(new Comparator<Point>(){
/* 두 값을 처리한 리턴 결과가 음수,0,양수 이냐에 따라 첫번 째 인자의 정렬순위가 낮음, 같음,높음으로 정의된다.
compare(Product o1, Product o2)
ex) o1(1), 02(99)일 경우
return o2-o1일 때 return 결과가 양수임으로 o1의 우선순위가 더 높다(내림차순)
ex) o1(1), o2(99)일 경우
reutrn o1-o2일 때는 return 결과가 음수이므로 o1의 우선순위가 더 낮다(오름차순)
*/
public int compare(Point second, Point third){
int ccwR = ccw(first, second, third);
if(ccwR > 0) // 반시계
return -1; // 오름차순
else if (ccwR < 0)
return 1; // 내림차순
else if (ccwR == 0){
long distR1 = dist(first, second);
long distR2 = dist(first, third);
if(distR1 > distR2)
return 1;
}
return -1;
}
});
// 그라함 스캔 알고리즘
Stack<Point> stack = new Stack<Point>();
stack.add(first);
for(int i=1; i<points.size(); i++){
// 시계방향이면 제거한다.
while(stack.size() > 1 && ccw(stack.get(stack.size()-2), stack.get(stack.size()-1), points.get(i)) <= 0){
stack.pop();
}
stack.add(points.get(i));
}
bw.write(stack.size() + "\n");
bw.flush();
br.close();
bw.close();
}
// ccw알고리즘 => 시계방향:-1, 일직선:0, 반시계:1
static int ccw(Point a, Point b, Point c){
long ccwR = (a.x*b.y + b.x*c.y + c.x*a.y) - (b.x*a.y + c.x*b.y + a.x*c.y);
if(ccwR > 0)
return 1;
if(ccwR < 0)
return -1;
return 0;
}
static long dist(Point a, Point b){
return (b.x-a.x)*(b.x-a.x) + (b.y-a.y)*(b.y-a.y);
}
static class Point{
long x, y;
public Point(long x, long y){
this.x = x;
this.y = y;
}
}
}'알고리즘 > [ Baekjoon ]' 카테고리의 다른 글
| [ BOJ ][JAVA][1018] 체스판 다시 칠하기 (0) | 2021.04.17 |
|---|---|
| [ Baekjoon ][JAVA][7812] 중앙 트리 (0) | 2020.10.20 |
| [ Baekjoon ][JAVA][6086] 최대유량 (0) | 2020.09.23 |
| [ Baekjoon ][JAVA][2188] 축사배정 (0) | 2020.09.23 |
| [ Baekjoon ][JAVA][1789] 수들의 합 (0) | 2020.09.22 |